
In our Acoustophoretic Force blog series, we have discussed the nature of acoustic radiation force and different ways to compute this force in the COMSOL Multiphysics® software. Today, we will introduce you to a related phenomenon, acoustic orbital angular momentum, and demonstrate how to model it.
The Sonic Screwdriver
Since first appearing on television in 1963, the Doctor Who® television show has followed the space and time travels of “the Doctor”. When boarding his time-traveling spaceship — a blue British police telephone box called TARDIS® console, as fans may already know — the Doctor often brings along new companions to share in his adventures as well as a valuable resource: the sonic screwdriver.
As its name suggests, the sonic screwdriver operates through sound waves that generate forces on objects at a distance. For the Doctor, this tool has proven particularly useful in a variety of situations, from lock picking to disarming weapons. The functions of the sonic screwdriver may be imaginary, but the physics behind its operation is based on a real concept.

The sonic screwdriver from the Doctor Who® television show. Image by Sonicdrewdriver, CC BY-SA 3.0, via Wikimedia Commons.
Acoustic radiation force, as we’ve previously highlighted on the blog, is a phenomenon that arises from the nonlinear response of a particle to an incident acoustic wave. A small fraction of the linear momentum carried by the wave is irreversibly absorbed by a particle, resulting in a net force. Like the linear momentum, the acoustic orbital angular momentum (OAM) is irreversibly absorbed by a solid object due to nonlinear effects, resulting in a net torque. This phenomenon has been observed experimentally when torque is applied to solid disks and microparticles.
Here, we will analyze acoustic OAM with the help of COMSOL Multiphysics.
Understanding Acoustic Orbital Angular Momentum
Acoustic wave simulations are the results of solutions of the wave equations. Certain classes of solutions for these equations admit fields with an orbital angular momentum associated with acoustic vortices. Such fields can be naturally realized in devices with cylindrical symmetry and identified by a phase singularity with respect to the symmetry axis. A phase term of the form \text{e}^{im\phi} is used to express the singularity. In this case, \phi is the azimuthal angle and m is an integer (called a topological charge), such that the phase is a multivalued function on the axis r= 0.
Let’s consider a practical device that can produce acoustic vortices, such as a circular ultrasonic array. The device (shown below) consists of a circular array of radially polarized PZT transducers in which each array element can be energized independently. The volume inside of the transducer ring can be filled with any liquid (e.g., water). The generator used to energize the array controls the phase and amplitude of the voltage that is applied to each element. As such, there is a high level of control over the acoustic fields generated inside of the fluid volume.
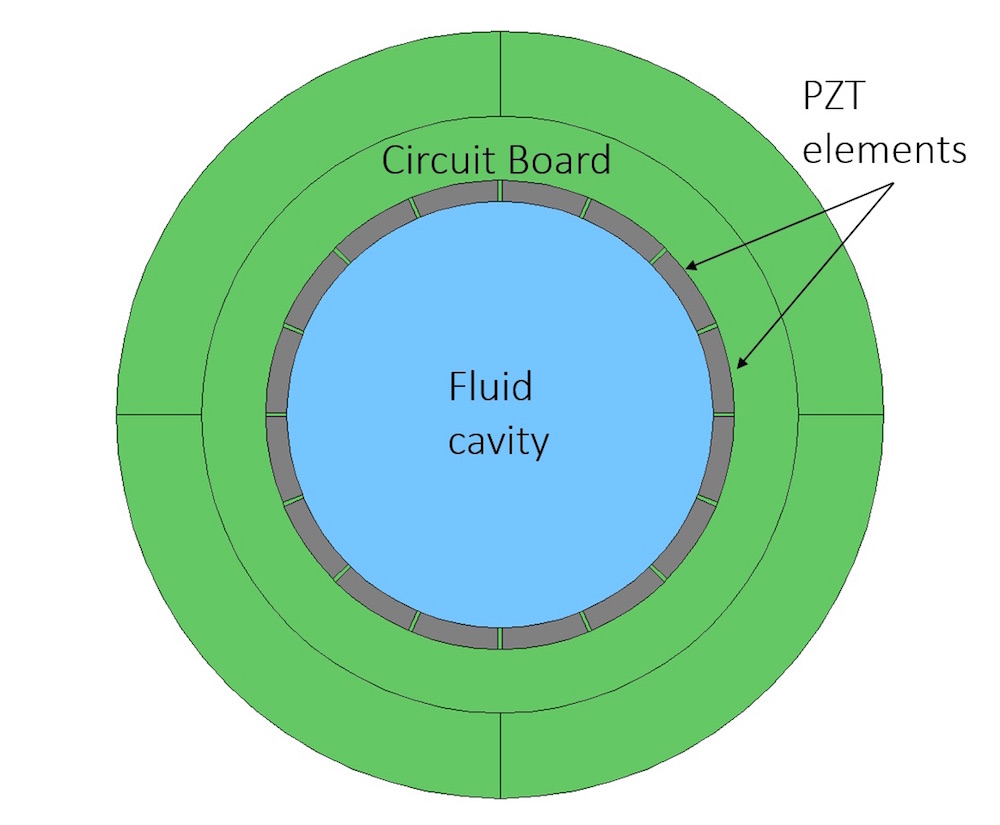
Schematic of a 16-element circular ultrasonic array device.
The Bessel field modes are the easiest field distributions that can be realized in this arrangement. These modes correspond to standing wave fields in which the radial distribution of the amplitude is defined by a Bessel function of the first kind J_m(kr), where k=2\pi/\lambda is the wave number corresponding to the wavelength \lambda. Meanwhile, the angular dependence of the field is exponential of the corresponding order m, such that the pressure distribution in the fluid is p(r,\phi) \propto J_m(kr)\text{e}^{im\phi}.
A pure Bessel field distribution is achieved near the center of the fluid volume. The field distribution becomes distorted by higher order modes — a result of aliasing effects that arise from the finite number of elements in the array that are some distance away from the center. In this solution, it is the exponential phase term that determines the amount of orbital angular momentum within the acoustic field. To excite the mth order of the acoustic field, the transducers are energized with a phase difference of 2\pi m/N (N is the number of elements) between the adjacent elements of the array. A rotating acoustic field is illustrated in the animation below.
The m=1 Bessel mode generated in a 16-element circular ultrasonic array device. The internal radius is 0.5 cm, with a frequency of 1.2 MHz corresponding to a 1.23 mm wavelength.
Is It Drag Force or Orbital Angular Momentum Transfer?
When microparticles are introduced into the rotating Bessel field, two acoustic forces and a torque resulting from OAM transfer will be exerted on them. The first force, acting in the radial direction, is a direct acoustic radiation force that pulls the particles to the nodes of the Bessel field. The second force acts in the azimuthal direction and is an indirect contribution of the acoustic radiation force. The flow circulation induced from the acoustic streaming effect produces the latter of these forces. In a previous blog post, we explained the modeling of this effect in COMSOL Multiphysics.
The combination of these two forces prompts the particles to move in a spiral motion. The spiral converges toward the axis in the central part of the fluid volume.
Particle trajectories in the central part of the fluid volume. Particles are pulled toward the nodes of the Bessel function, with rotation resulting from the viscous drag in the acoustic streaming flow.
The particle trajectories in the above animation were computed with the Drag Force and Acoustic Radiation nodes, available in the Particle Tracing for Fluid Flow interface in COMSOL Multiphysics. The input fields for evaluating these forces were obtained from the solution of the acoustic field distribution (from the Thermoacoustics interface) and the fluid flow field distribution (from the Laminar Flow interface, with volume forces from the acoustic fields). While the drag force can account for the rotation of the particles off of the axis, the particles’ radial velocity decreases as they approach the axis, such that the radial velocity of the cluster of particles at the center is zero. This is expected, as the fluid cannot support a singularity at the axis. Thus, the radial velocity must approach zero on the axis.
Such results contradict experimental observations in which the cluster of particles at the center was shown to rotate with considerable angular velocity. This suggests that while the two forces considered in producing this animation can account for the behavior of isolated particles away from the axis, they do not sufficiently explain the rotation of the cluster at the axis. These results only apply when computing forces on isolated small particles.
To explain the observed rotation, we must consider two additional effects originating in the size of the particle cluster in the center. In such a cluster/particle, both the acoustically absorbed OAM and the viscous drag force would be larger than in a small particle. Nevertheless, the underlying source of these forces is the acoustic field, such that both effects can be viewed as different mechanisms by which the OAM of the acoustic field is transferred to the cluster of particles.
The transfer of acoustic OAM to particles has been observed in a number of experiments in which different devices produced acoustic vortices. In this blog post, we have only considered one of the many examples. Whether or not this is the technology that will arm the Doctor with a sonic screwdriver remains to be seen in the future (or in the past).
Other Posts in This Series
- How to Compute the Acoustic Radiation Force
- Direct FSI Approach to Computing the Acoustic Radiation Force
Further Reading
- Blog post: A Thermoviscous Analysis of Acoustic Radiation Forces
- Z. Hong, J. Zhang, and B. W. Drinkwater, “Observation of Orbital Angular Momentum Transfer from Bessel-Shaped Acoustic Vortices to Diphasic Liquid-Microparticle Mixtures“, Phys. Rev. Lett. 114, 214301
- A. Anhäuser, R. Wunenburger, and E. Brasselet, “Acoustic Rotational Manipulation Using Orbital Angular Momentum Transfer“, Phys. Rev. Lett. 109, 034301
- F. G. Mitri, T. P. Lobo, and G. T. Silva, “Axial acoustic radiation torque of a Bessel vortex beam on spherical shells“, Phys. Rev. E 84, 065601(R)
- A. Grinenko, P. D. Wilcox, C. R. P. Courtney, and B. W. Drinkwater, “Proof of principle study of ultrasonic particle manipulation by a circular array device“, Proc. R. Soc. A doi:10.1098/rspa.2012.0232
Doctor Who and TARDIS are registered trademarks of The British Broadcasting Corporation (BBC). BBC is not affiliated with, connected to, or associated with COMSOL and has not produced, sponsored, or approved COMSOL’s software or this content.



Comments (0)