
The Domain Decomposition solver is a memory-efficient iterative algorithm with inherent parallelism on the geometric level. We can use this method to compute large modeling problems that can’t be solved with other direct or iterative methods. This solver’s primary field of application is on clusters, but it can also enable the solution of large problems on laptops and workstations. Let’s see how to use this functionality in the COMSOL Multiphysics® software.
Exploring the Schwarz-Type Domain Decomposition Solver
The Domain Decomposition solver is based on a decomposition of the spatial domain into overlapping subdomains, where the subdomain solutions are less complex and more efficient in terms of memory usage and parallelization compared to the solution of the original problem.
In order to describe the basic idea of the iterative spatial Domain Decomposition solver, we consider an elliptic partial differential equation (PDE) over a domain D and a spatial partition {Di}i, such that the whole domain D = UiDi is covered by the union of the subdomains Di. Instead of solving the PDE on the entire domain at once, the algorithm iteratively solves a number of problems for each subdomain Di.
For Schwarz-type domain decomposition methods, the subdomains encompass an overlap of their support in order to transfer the information. On the interfaces between the subdomains, the solutions of the neighboring subdomains are used to update the current subdomain solution. For instance, if the subdomain Di is adjacent to a boundary, its boundary conditions are used. The iterative domain decomposition procedure is typically combined with a global solver on a coarser mesh in order to accelerate convergence.

A 2D domain with a regular triangular mesh and its degrees of freedom decomposed into quadratic subdomains.
To illustrate the spatial domain decomposition, consider a 2D regular triangular mesh. For simplicity, we consider linear finite element shape functions with degrees of freedom in the 3 nodes of the triangular elements. The domain (more precisely, its degrees of freedom) is decomposed into quadratic subdomains, each consisting of 25 degrees of freedom. All interior subdomains have 8 neighboring subdomains and all degrees of freedom are unique to a single subdomain. The support of the linear element functions for a single subdomain is overlapping with the support of its neighbors.
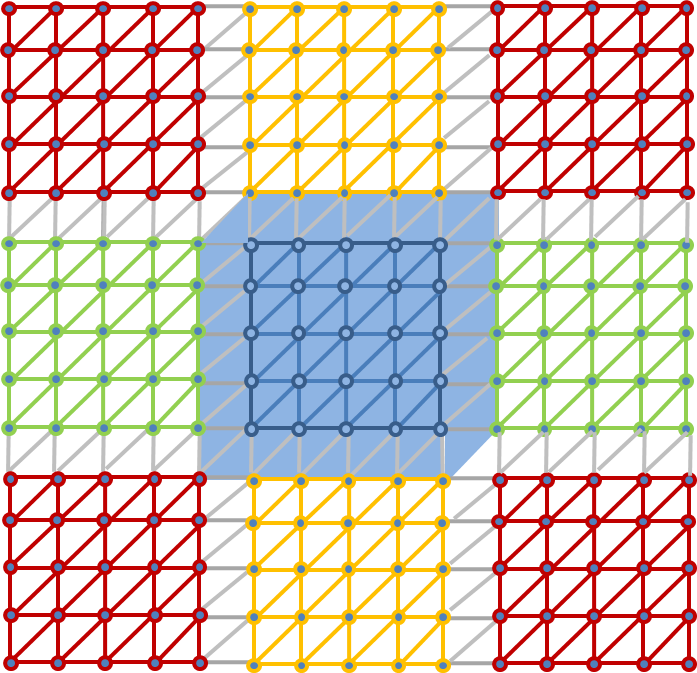
Support of the linear element functions of the blue subdomain.
To improve the convergence rate of the iterative procedure, we may need to include a larger number of degrees of freedom in order to have a larger overlap of the subdomain support. This may give a more efficient coupling between the subdomains and a lower iteration count until convergence of the iterative procedure. However, this benefit comes at the costs of additional memory usage and additional computations during the setup and solution phase because of the larger subdomain sizes.
If an additional overlap of width 1 is requested, we add an additional layer of degrees of freedom to the existing subdomain. In our example, 22 degrees of freedom (marked with blue rectangles) are added to the blue subdomain. The support of the blue subdomain is enlarged accordingly.
The same procedure is repeated for the red, green, and yellow subdomains. In the resulting subdomain configuration, some of the degrees of freedom are unique to a single subdomain, while others are shared by two, three, or even four subdomains. It is obvious that dependencies arise for the shared degrees of freedom if one of its adjacent subdomains updates its solution.
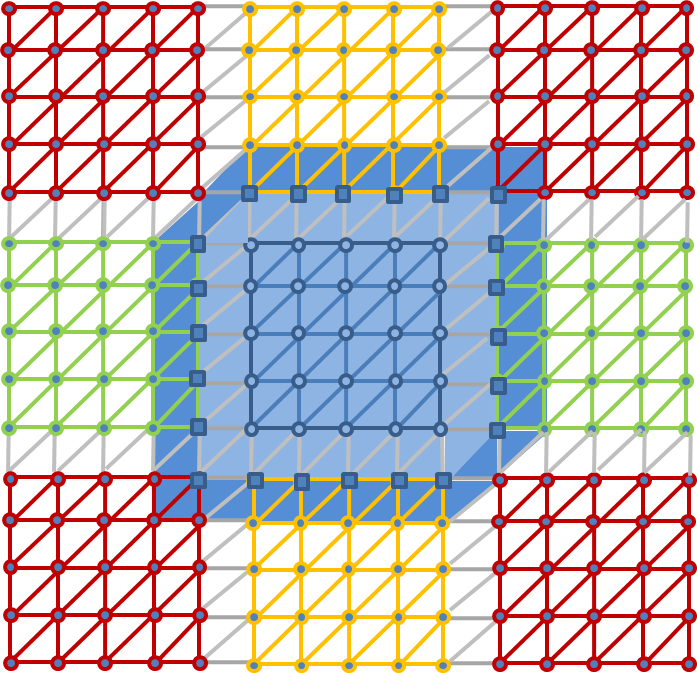
Extended subdomain with 47 degrees of freedom and its support. The additional 22 degrees of freedom are shared with the neighboring subdomains.
It is known (Ref. 1) that the iterative solution to the set of subdomain problems on the subdomains, Di, converges toward the solution of the original problem formulated over the whole domain D. Hence, the global solution can be found by iteratively solving each subdomain problem with all other domains fixed until the convergence criteria is met. The optional coarse grid problem can improve the convergence rate considerably. The coarse grid problem, which is solved on the entire domain D, gives an estimate of the solution on the fine grid on D and can transfer global information faster. The convergence rate of the method depends on the ratio between the size of the coarse grid mesh elements and the width of the overlap zone on the fine grid.
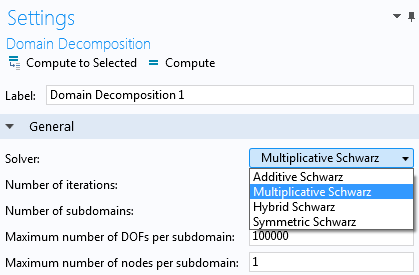
If we compute the solution on a particular subdomain Di, the neighboring subdomains need to update their degrees of freedom adjacent to the support of Di. In COMSOL Multiphysics, there are four options available for the coordination of the subdomain overlap and the global coarse grid solution. The selector Solver in the domain decomposition settings can be set to Additive Schwarz, Multiplicative Schwarz (default), Hybrid Schwarz, and Symmetric Schwarz. For Additive Schwarz methods, the affected degrees of freedom are updated after all solutions have been computed on all subdomains without an intermediate data exchange. In this case, the order of the subdomain solutions is arbitrary and there are no dependencies between the subdomains during this solution phase.
In contrast, Multiplicative Schwarz methods update the affected degrees of freedom at the overlap of the support of neighboring subdomains after every subdomain solution. This typically speeds up the iterative solution procedure. However, there is an additional demand for prescribing an order of the subdomain solutions, which are no longer fully independent of each other.
The Hybrid Schwarz method updates the solution after the global solver problem is solved. The subdomain problems are then solved concurrently as in the Additive Schwarz solver case. The solution is then updated again and the global solver problem is solved a second time. The Symmetric Schwarz method solves the subdomain problems in a given sequence like the Multiplicative Schwarz solver, but in a symmetric way.
Direct Solvers and Preconditioned Iterative Solvers
Direct linear solvers are typically more robust and require less tweaking of the physics-dependent settings than iterative solvers with tuned preconditioners. Due to their memory requirements, however, direct solvers may become unfeasible to use for larger problems. Iterative solvers are typically leaner in memory consumption, but some models still can’t be solved due to resource limitations. We discuss the memory requirements for solving large models in a previous blog post. Other preconditioners for iterative solvers may also fail due to specific characteristics of the system matrix. Domain decomposition is a preconditioner that in many cases requires less tuning than other preconditioners.
In case of limitations by the available memory, we can move the solution process to a cluster that provides a larger amount of accumulated memory. We can consider the domain decomposition preconditioner, using a domain solver with settings that mimic the original solver settings, since the Domain Decomposition solver has the potential to do more concurrent work. As we will see, the Domain Decomposition solver can also be used in a Recompute and clear mode, where you can get a significant memory reduction, even on a workstation.
If we do not want to use an additional coarse mesh to construct the global solver, we can compute its solution using an algebraic method. This may come at the price of an increased amount of GMRES iterations compared to when we set the Use coarse level selector to Geometric, which is based on an additional coarser mesh. The advantage is that the algebraic method constructs the global solver from the finest-level system matrix, and not by means of an additional coarser mesh. With the Algebraic option, the generation of an additional coarse mesh, which might be costly or not even possible, can be avoided.
Domain Decomposition Preconditioning on a Cluster
On a cluster, a subdomain problem can be solved on a single node (or on a small subset of the available nodes). The size of the subdomains, hence the memory consumption per node, can be controlled by the Domain Decomposition solver settings. For the Additive Schwarz solver, all subdomain problems can be solved concurrently on all nodes. The solution updates at the subdomain interfaces occur in the final stage of the outer solver iteration.
For the Multiplicative Schwarz solver, there are intermediate updates of the subdomain interface data. This approach can speed up the convergence of the iterative procedure, but introduces additional dependencies for the parallel solution. We must use a subdomain coloring mechanism in order to identify a set of subdomains that can be processed concurrently. This may limit the degree of parallelism if there is a low number of subdomains per color. In general, the Multiplicative Schwarz and Symmetric Schwarz methods converge faster than the Additive Schwarz and Hybrid Schwarz methods, while these methods can result in better parallel speedup.

A subdomain coloring mechanism is used for multiplicative Schwarz-type domain decomposition preconditioning.
In the Domain Decomposition solver settings, there is a Use subdomain coloring checkbox for the Multiplicative Schwarz and Hybrid Schwarz methods. This option is enabled by default and takes care of grouping subdomains into sets — so-called colors — that can be handled concurrently. Let us consider a coloring scheme with four colors (blue, green, red, and yellow). All subdomains of the same color can compute their subdomain solution at the same time and communicate the solution at the subdomain overlap to their neighbors. For four colors, the procedure is repeated four times until the global solution can be updated.
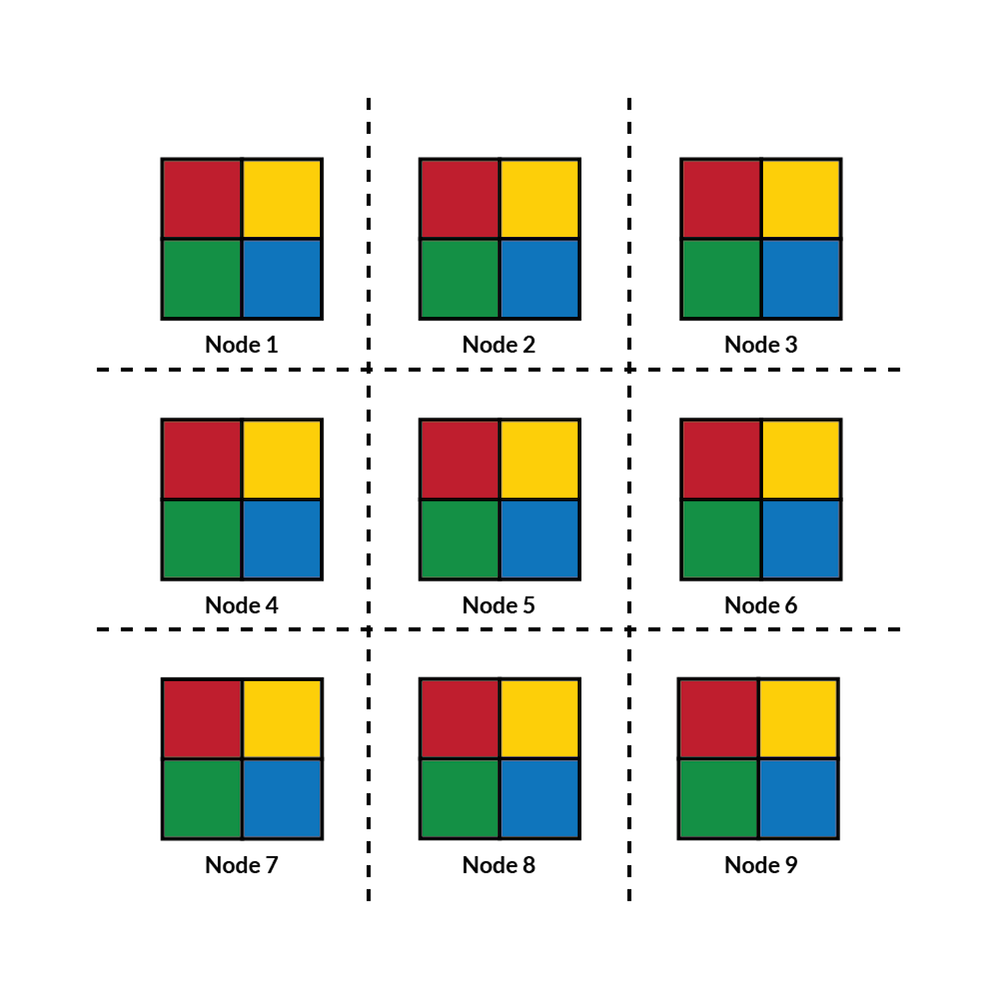
Domain decomposition on a cluster with nine nodes. A subdomain coloring scheme is used to compute subdomain solutions simultaneously for each different color.
On a cluster, the subdomains can be distributed across the available compute nodes. Every color can be handled in parallel and all of the nodes compute their subdomain solutions for the current color at the same time and then proceed with the next color. The coloring scheme coordinates the order of the subdomain updates for the Multiplicative Schwarz and Symmetric Schwarz methods. Communication is required for updating the degrees of freedom across the compute node boundaries in between every color. No subdomain coloring scheme is required for the Additive Schwarz and Hybrid Schwarz methods.
The different Domain Decomposition solver types.
What About Nondistributed Cases?
If the Domain Decomposition solver is run on a single workstation, all data needs to be set up in the same memory space and there is no more benefit from storing only specific subdomain data. Due to the subdomain overlap, the memory consumption might even increase compared to the original problem. In order to overcome this limitation, the Domain Decomposition solver can be run in the Recompute and clear mode, where the data used by each subdomain is computed on the fly. This results in a significant memory reduction and solves larger problems without needing to store the data in virtual memory. These problems will take longer to compute due to repeated setup of the subdomain problems.
This method is particularly useful when the solution uses a lot of virtual memory with disk swapping. If the Automatic option is used, the Recompute and clear mechanism is activated if there is an out-memory error during the setup phase. The setup is then repeated with Recompute and clear activated. The Recompute and clear option is comparable to the out-of-core option of the direct solvers. Both methods have an additional penalty; either because of storing additional data to the disk (Out-of-core) or because of recomputing specific parts of the data again and again (Recompute and clear). We can save even more memory by using the matrix-free format on top of the Recompute and clear option.
Tuning the Domain Decomposition Solver
In the settings of the Domain Decomposition solver, we can specify the intended Number of subdomains (see the figure below). In addition, the Maximum number of DOFs per subdomain is specified. If the latter bound is missed — i.e., one of the subdomains has to handle more degrees of freedom than specified — then all subdomains are recreated, taking a larger number of subdomains.
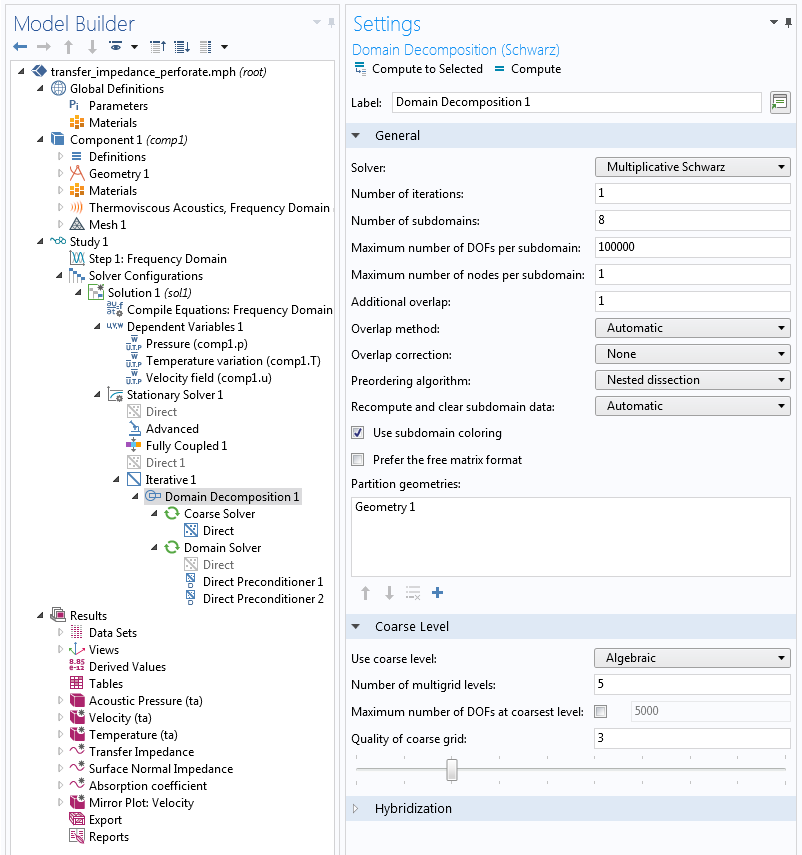
Settings window for the Domain Decomposition solver.
The subdomains are created by means of the element and vertex lists taken from the mesh. We are able to choose from different subdomain ordering schemes. The Nested Dissection option creates a subdomain distribution by means of graph partitioning. This option typically gives a low number of colors and results in balanced subdomains with an approximately equal number of degrees of freedom, minimal subdomain interfaces, and a small overlap.
An alternative method that also avoids slim domains is to use the Preordering algorithm based on a Space-filling curve. If we select the option None for the Preordering algorithm, the subdomain ordering is based on the ordering of the mesh elements and degrees of freedom. This can result in slim domains. Detailed information about the applied subdomain configuration is given in the solver log if the Solver log on the Advanced node is set to Detailed.
Summary on Using the Domain Decomposition Solver in COMSOL Multiphysics®
When simulating problems with large memory requirements in the COMSOL® software, we are limited by the available hardware resources. An iterative solver with domain decomposition preconditioning should be considered as a memory-lean alternative to direct solvers. On a workstation, the Recompute and clear option for the Domain Decomposition solver is an alternative to the out-of-core mechanism for the direct solvers.
Although memory-heavy simulations can fail on computers with insufficient memory, we can enable them on clusters. The direct solvers in COMSOL Multiphysics automatically use the distributed memory, leading to a memory reduction on each node. The Domain Decomposition solver is an additional option that takes advantage of the parallelization based on the spatial subdomain decomposition.
The Domain Decomposition solver, clusters, and a variety of the options discussed here will help you improve computational efficiency when working with large models in COMSOL Multiphysics. In an upcoming blog post, we will demonstrate using the domain decomposition preconditioner in a specific application scenario. Stay tuned!
Check Out More Resources on Solvers
- Find more information on optimizing your simulation’s computational methods and memory requirements in the Solvers category on the COMSOL Blog
- Browse updates to the studies and solvers included with COMSOL Multiphysics version 5.2a, including the improved capabilities of the Domain Decomposition solver, on the Release Highlights page
Reference
-
A. Toselli and O. Widlund, “Domain Decomposition Methods — Algorithms and Theory,” Springer Series in Computational Mathematics, vol. 34, 2005.




Comments (3)
海 林
January 8, 2017hi, Jan-Philipp Weiss,
it is very helpful for the application of domain decomposition method (DDM) in COMSOL for solving large problems. I am new to DDM, and i am curious about how can COMSOL display the partitioned geometry (or mesh) . You know, for some reasons, i would like to known these things.
Best regards!
Jan-Philipp Weiss
January 13, 2017Hi,
Thank you for your question. In the current version of COMSOL Multiphysics® there is no option for a visualization of the subdomain partitioning. We are aware that this feature can be helpful and have already discussed to add it in one of the next releases.
Best regards,
Jan-Philipp Weiss
Mohammad Aghababaei
October 9, 2020Dear Jan-Philipp Weiss,
I am working on modeling solute transport in the river by considering the mass exchange between the main flow and the hyporheic zone (a zone below the river bed). The length of the domain of my study is about 30 kilometers. My question here is that how can I use Domain Decomposition Solver to model my problem in a very small subdomain (with around 10 meters length) and then use the results of that to simulate the problem over the whole domain? The general idea here is that for each subdomain, the outflow concentration distribution over the y-axis should be the inflow for the next right neighboring subdomain.
Kind Regards,
Mohammad