General Blog Posts
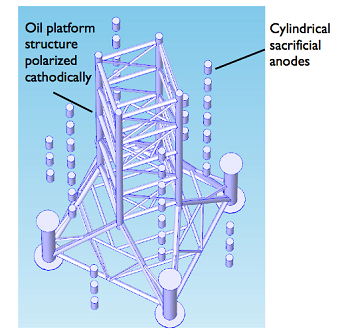
Intro to Corrosion Modeling for the Oil and Gas Industry
From impressed cathodic current and anodic protection to sacrificial anodes, there are several ways you can protect structures from corrosion. We discuss some modeling considerations here.
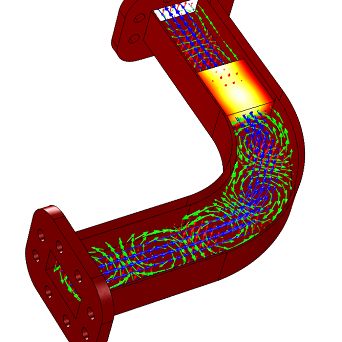
Quick Intro to Modeling RF and Microwave Heating
If you’ve attended a COMSOL webinar about an RF topic, you’ve probably seen our model of a waveguide with a bend. That’s because it illustrates microwave heating in an easy-to-understand way.

Intro Model: Studying the Signal Strength of RF Coils
Electronics designers need to ensure that RF coils contained within their devices can properly transmit information from a source to its destination. Electromagnetics simulation can help.
How to Integrate Functions Without Knowing the Limits of the Integral
Did you know that the COMSOL® software can solve integrals as well as partial differential equations? Learn how to integrate functions — even without knowing the limits of the integral.

The Strength of the Weak Form
Learn about the origins of the weak form equations, how to derive them from classic equations, how to express them in the COMSOL Multiphysics® syntax, and more >>
Geometric Kernels in COMSOL Multiphysics®
Do you know what a geometric kernel is? This software component is responsible for handling geometry in COMSOL Multiphysics®. Get a comprehensive background of what this means…

Building a Beowulf Cluster for Faster Multiphysics Simulations
In 1994, NASA researchers built a small cluster of normal workstations. They called this parallel workstation Beowulf. Today, “Beowulf cluster” describes clusters built from normal workstations.
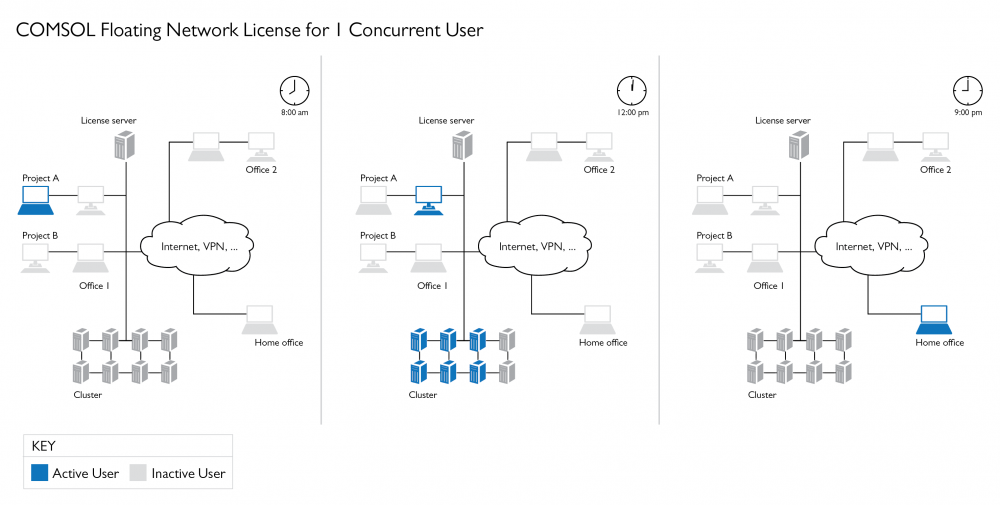
How Do I Get the Most out of My Floating Network License (FNL)?
What’s the different between a COMSOL CPU-Locked Single User (CPU) and Floating Network License (FNL)? We discuss these differences and go over how to get the most out of your FNL.
