
In this blog post we will explain the concept of conjugate heat transfer and show you some of its applications. Conjugate heat transfer corresponds with the combination of heat transfer in solids and heat transfer in fluids. In solids, conduction often dominates whereas in fluids, convection usually dominates. Conjugate heat transfer is observed in many situations. For example, heat sinks are optimized to combine heat transfer by conduction in the heat sink with the convection in the surrounding fluid.
Heat Transfer by Solids and Fluids
Heat Transfer in a Solid
In most cases, heat transfer in solids, if only due to conduction, is described by Fourier’s law defining the conductive heat flux, q, proportional to the temperature gradient: q=-k\nabla T.
For a time-dependent problem, the temperature field in an immobile solid verifies the following form of the heat equation:
Heat Transfer in a Fluid
Due to the fluid motion, three contributions to the heat equation are included:
- The transport of fluid implies energy transport too, which appears in the heat equation as the convective contribution. Depending on the thermal properties on the fluid and on the flow regime, either the convective or the conductive heat transfer can dominate.
- The viscous effects of the fluid flow produce fluid heating. This term is often neglected, nevertheless, its contribution is noticeable for fast flow in viscous fluids.
- As soon as a fluid density is temperature-dependent, a pressure work term contributes to the heat equation. This accounts for the well-known effect that, for example, compressing air produces heat.
Accounting for these contributions, in addition to conduction, results in the following transient heat equation for the temperature field in a fluid:
Conjugate Heat Transfer Applications
Effective Heat Transfer
Efficiently combining heat transfer in fluids and solids is the key to designing effective coolers, heaters, or heat exchangers.
The fluid usually plays the role of energy carrier on large distances. Forced convection is the most common way to achieve high heat transfer rate. In some applications, the performances are further improved by combining convection with phase change (for example liquid water to vapor phase change).
Even so, solids are also needed, in particular to separate fluids in a heat exchanger so that fluids exchange energy without being mixed.
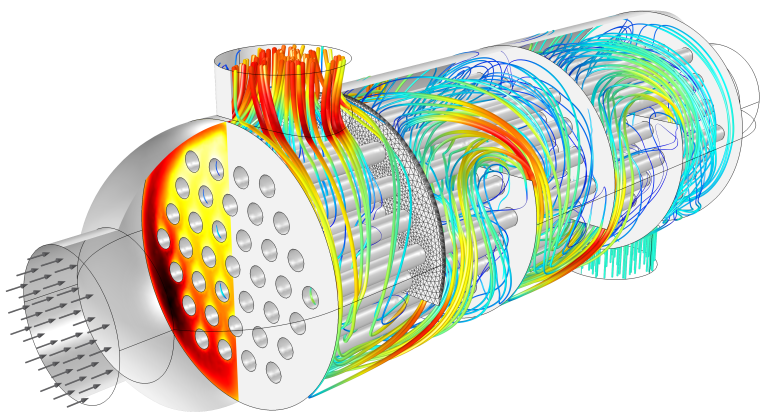
Flow and temperature field in a shell-and-tube heat exchanger illustrating heat transfer between two fluids separated by the thin metallic wall.
Heat sinks are usually made of metal with high thermal conductivity (e.g. copper or aluminum). They dissipate heat by increasing the exchange area between the solid part and the surrounding fluid.

Temperature field in a power supply unit cooling due to an air flow generated by an extracting fan and a perforated grille. Two aluminum fins are used to increase the exchange area between the flow and the electronic components.
Energy Savings
Heat transfer in fluids and solids can also be combined to minimize heat losses in various devices. Because most gases (especially at low pressure) have small thermal conductivities, they can be used as thermal insulators… provided they are not in motion. In many situations, gas is preferred to other material due to its low weight. In any case, it is important to limit the heat transfer by convection, in particular by reducing the natural convection effects. Judicious positioning of walls and use of small cavities helps to control the natural convection. Applied at the micro scale, the principle leads to the insulation foam concept where tiny cavities of air (bubbles) are trapped in the foam material (e.g. polyurethane), which combines high insulation performances with light weight.
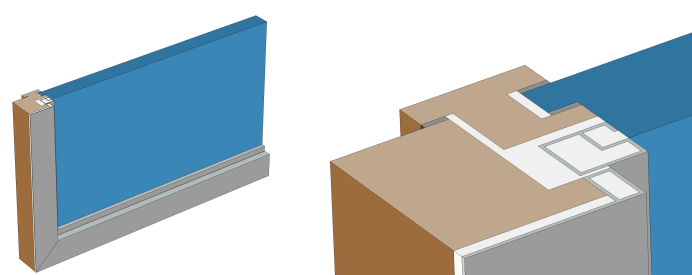
Window cross section (left) and zoom-in on the window frame (right).
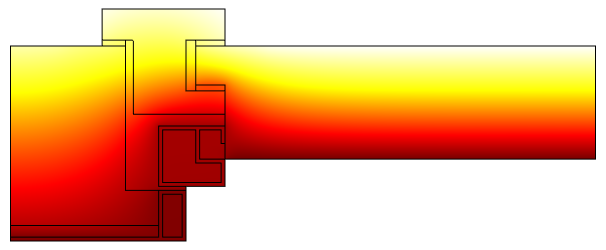
Temperature profile in a window frame and glazing cross section from ISO 10077-2:2012 (thermal performance of windows).
Fluid and Solid Interactions
Fluid/Solid Interface
The temperature field and the heat flux are continuous at the fluid/solid interface. However, the temperature field can rapidly vary in a fluid in motion: close to the solid, the fluid temperature is close to the solid temperature, and far from the interface, the fluid temperature is close to the inlet or ambient fluid temperature. The distance where the fluid temperature varies from the solid temperature to the fluid bulk temperature is called the thermal boundary layer. The thermal boundary layer size and the momentum boundary layer relative size is reflected by the Prandtl number (Pr=C_p \mu/k): for the Prandtl number to equal 1, thermal and momentum boundary layer thicknesses need to be the same. A thicker momentum layer would result in a Prandtl number larger than 1. Conversely, a Prandtl number smaller than 1 would indicate that the momentum boundary layer is thinner than the thermal boundary layer. The Prandtl number for air at atmospheric pressure and at 20°C is 0.7. That is because for air, the momentum and thermal boundary layer have similar size, while the momentum boundary layer is slightly thinner than the thermal boundary layer. For water at 20°C, the Prandtl number is about 7. So, in water, the temperature changes close to a wall are sharper than the velocity change.
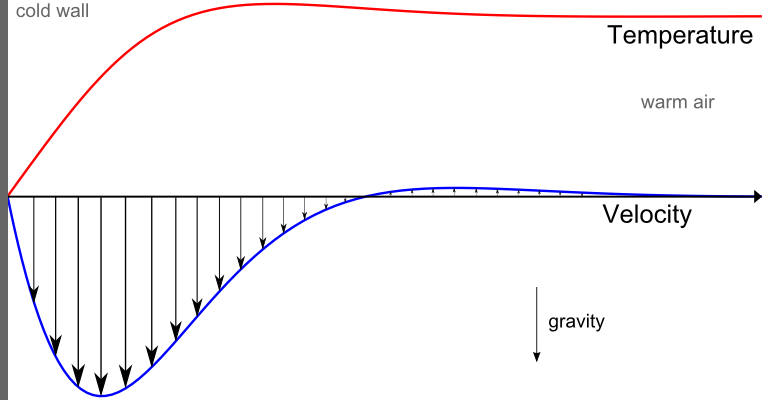
Normalized temperature (red) and velocity (blue) profile for natural convection of air close to a cold solid wall.
Natural Convection
The natural convection regime corresponds to configurations where the flow is driven by buoyancy effects. Depending on the expected thermal performance, the natural convection can be beneficial (e.g. cooling application) or negative (e.g. natural convection in insulation layer).
The Rayleigh number, noted as Ra, is used to characterized the flow regime induced by the natural convection and the resulting heat transfer. The Rayleigh number is defined from fluid material properties, a typical cavity size, L, and the temperature difference,\Delta T, usually set by the solids surrounding the fluid:
The Grashof number is another flow regime indicator giving the ratio of buoyant to viscous forces:
The Rayleigh number can be expressed in terms of the Prandtl and the Grashof numbers through the relation Ra=Pr Gr.
When the Rayleigh number is small (typically <103), the convection is negligible and most of the heat transfer occurs by conduction in the fluid.
For a larger Rayleigh number, heat transfer by convection has to be considered. When buoyancy forces are large compared to viscous forces, the regime is turbulent, otherwise it is laminar. The transition between these two regimes is indicated by the critical order of the Grashof number, which is 109. The thermal boundary layer, giving the typical distance for temperature transition between the solid wall and the fluid bulk, can be approximated by \delta_\mathrm{T} \approx \frac{L}{\sqrt[4\,]{Ra}} when Pr is of order 1 or greater.

Temperature profile induced by natural convection in a glass of cold water in contact with a hot surface .
Forced Convection
The forced convection regime corresponds to configurations where the flow is driven by external phenomena (e.g. wind) or devices (e.g. fans, pumps) that dominate buoyancy effects.
In this case the flow regime can be characterized, similarly to isothermal flow, using the Reynolds number as an indicator,Re= \frac{\rho U L}{\mu}. The Reynolds number represents the ratio of inertial to viscous forces. At low Reynolds numbers, viscous forces dominate and laminar flow is observed. At high Reynolds numbers, the damping in the system is very low, giving small disturbances. If the Reynolds number is high enough, the flow field eventually ends up in turbulent regime.
The momentum boundary layer thickness can be evaluated, using the Reynolds number, by \delta_\mathrm{M} \approx \frac{L}{\sqrt{Re}}.
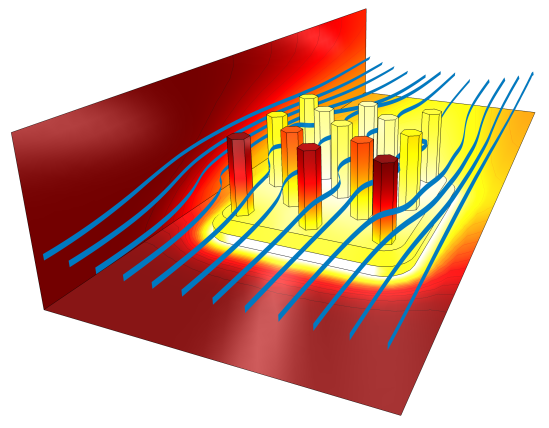
Streamlines and temperature profile around a heat sink cooling by forced convection.
Radiative Heat Transfer
Radiative heat transfer can be combined with conductive and convective heat transfer described above.
In a majority of applications, the fluid is transparent to heat radiation and the solid is opaque. As a consequence, the heat transfer by radiation can be represented as surface-to-surface radiation transferring energy between the solid wall through transparent cavities. The radiative heat flux emitted by a diffuse gray surface is equal to \varepsilon n^2 \sigma T^4. When a surface is surrounded by bodies at a homogeneous T_\mathrm{amb}, the net radiative flux is q_\mathrm{r} = \varepsilon n^2 \sigma (T_\mathrm{amb}^4-T^4). When surrounding surfaces of different temperatures, each surface-to-surface exchange is determined by the surface’s view factors.
Nevertheless, both fluids and solids may be transparent or semitransparent. So radiation can occur in fluid and solids. In participating (or semitransparent) media, the radiation rays interact with the medium (solid or fluid) then absorb, emit, and scatter radiation.
Whereas radiative heat transfer can be neglected in applications with small temperature differences and lower emissivity, it plays a major role in applications with large temperature differences and large emissivities.
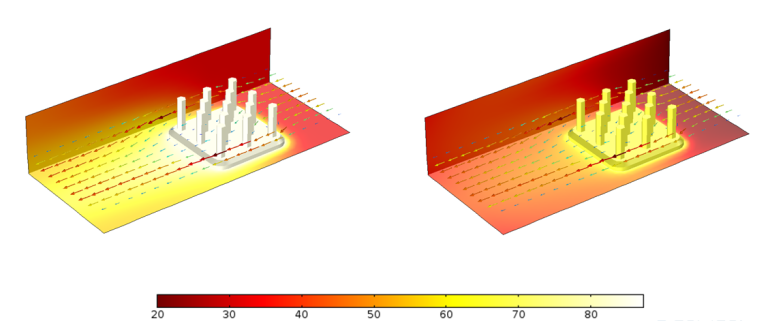
Comparison of temperature profiles for a heat sink with a surface emissivity \varepsilon = 0 (left) and \varepsilon = 0.9 (right).
Conclusion
Heat transfer in solids and heat transfer in fluids are combined in the majority of applications. This is because fluids flow around solids or between solid walls, and because solids are usually immersed in a fluid. An accurate description of heat transfer modes, material properties, flow regimes, and geometrical configurations enables the analysis of temperature fields and heat transfer. Such a description is also the starting point for a numerical simulation that can be used to predict conjugate heat transfer effects or to test different configurations in order, for example, to improve thermal performances of a given application.
Notations
C_{p}: heat capacity at constant pressure (SI unit: J/kg/K)
g: gravity acceleration (SI unit: m/s2)
Gr: Grashof number (dimensionless number)
k: thermal conductivity (SI unit: W/m/K)
L: characteristic dimension (SI unit: m)
n: refractive index (dimensionless number)
p_\mathrm{A}: absolute pressure (SI unit: Pa)
Pr: Prandtl number (dimensionless number)
q: heat flux (SI unit: W/m2)
Q: heat source (SI unit: W/m3)
Ra: Rayleigh number (dimensionless number)
S: strain rate tensor (SI unit: 1/s)
T: temperature field (SI unit:K)
T_\mathrm{amb}: ambient temperature (SI unit: K)
\bold{u}: velocity field (SI unit: m/s)
U: typical velocity magnitude (SI unit: m/s)
\alpha_{p}: thermal expansion coefficient (SI unit: 1/K)
\delta_\mathrm{M}: momentum boundary layer thickness (SI unit: m)
\delta_\mathrm{T}: thermal layer thickness (SI unit: m)
\Delta T: characteristic temperature difference (SI unit: K)
\varepsilon: surface emissivity (dimensionless number)
\rho: density (SI unit: kg/m3)
\sigma: Stefan-Boltzmann constant (SI unit: W/m2T4)
\tau: viscous stress tensor (SI unit: N/m2)






Comments (46)
ali hassan
January 15, 2014How can using conjugate heat transfer model in case flow boiling water through porous media ?
Nicolas Huc
January 20, 2014Conjugate heat transfer interface in COMSOL Multiphysics is dedicated to heat transfer in solids and non-isothermal flow for free flows. If the model scale is small enough (so that the porous cavities are explicitly represented), this interface may be used using a similar approach as shown in http://www.comsol.com/model/boiling-water-3972 .
Otherwise a porous media flow model should be used instead of the free flow model.
Ana Tostao
July 16, 2014Can I use Conjugate HT interface to simulate the air flow through a porous media? There is any example in COMSOL gallery?
Nicolas Huc
July 17, 2014Assuming local thermal equilibrium you can model heat transfer and flow in a porous media. A simple tutorial is available on http://www.comsol.com/model/free-convection-in-porous-medium-278, it shows how to set up a flow and a heat interfaces in porous media.
Hassanein Mobarek
November 10, 2014Hi,
I am willing to simulate soil sample that has a water resource from the bottom and a heat source from top, is the conjugate heat transfer is the best physics or not?
Hamla Ilyes
March 9, 2015hi sir
I try to make a geometry using COMSOL Multiphysics software, but I can not carry it out.
I am looking for someone to give me some ideas how to use this software ready
if you want to help me, I’ll send you the dimensions of this geometry.
Thank you in advance
ilyes
manik kumar
June 23, 2015hey i want to what physics do i choose for fluid flow over oscillating heated cylinder time dependent…..:)
manik kumar
June 23, 2015hey guys i want to knoe that what physics shall i use for the fluid flow over heated cylinder for lumped analysis
Nicolas Huc
August 13, 2015Dear Hassanein Mobarek,
In COMSOL Multiphysics 5.1, it is possible to simulate porous media flow using the Conjugate Heat Transfer interface. It’s definitely a good option.
Nicolas Huc
August 13, 2015Dear Manik Kumar,
The Conjugate Heat Transfer interface available in the Heat Transfer module and CFD module is suitable to model oscillating non-isothermal flow past a heated cylinder.
Pradeep Kumar M C
April 22, 2016Hi,
I am trying to study time dependent heat transfer b/w hot water and solid material. flow is turbulent i am confused which module should be used (conjugate or non isothermal) and need guidance. can anyone help.
Nicolas Huc
April 22, 2016Dear Pradeep Kumar,
Both interfaces can be used (they offer same functionalities but have different default settings). For your application I recommend to use the Conjugate Heat Transfer multiphysics interface. In COMSOL Multiphysics 5.2 you can choose between following turbulence models:
– Algebraic yPlus
– L-VEL
– k-ε
– k-ω
– SST
– Low Re – k-ε
– Spalart-Allmaras
Mohamed Lamine Amrani
May 10, 2016Hi;
i try to modling natural conviction in power transformer but i have probleme with gravity , please i need your helpe
Parth Swaroop
May 16, 2016It is necessary to explicitly have the non isothermal in the multi-physics node in order for laminar/turbulent flow to interact with heat transfer in fluid, even if they are assigned to the same domain?
Nicolas Huc
June 27, 2016Dear Mohamed,
In COMSOL Multiphysics v5.2a we have a predefined option to include gravity in the single phase flow interface. You just have to select this option to model natural convection in a non-isothermal flow.
Nicolas Huc
June 27, 2016Dear Parth,
The nonisothermal flow node couples the heat and the flow interfaces and provides options to account for viscous dissipation and pressure work. It is possible to define these couplings manually but using the predefined coupling is simpler. In addition the nonisothermal flow node tunes the stabilization of the flow and the heat interfaces for the coupling. Finally, it defines the thermal wall functions when wall functions are used by the turbulent flow model.
Yogeshwari Chandrawat
July 6, 2016i am trying to couple heat transfer between a hot solid cylinder and a cold fluid flowing inside it in a concentric cylinder. I tried using conjugate heat transfer model with laminar flow. However, i am unable to define 2 separate initial values of temperature for the solid and the cylinder. Am i applying the correct physics? if yes, how can i get 2 separate temperature profiles for the 2 different domains?
Nicolas Huc
July 6, 2016Dear Yogeshwari,
There are different mean to define different conditions on different domains. For this case I suggest to add a second Initial Value node Heat Transfer interface. The define the selection where you want to apply it. Thanks to that you can use 2 different expressions to define the initial conditions.
Qasim Ranjha
October 25, 2016Hi Nicolas,
I am trying to simulate heat transfer from porous domain to a fluid domain separated by a wall. Earlier I successfully used conjugate HT module assuming an interface condition between porous and fluid domains.
Now I want to add a wall with thermal resistance between the domains. Should I use conjugate HT module for this case as well ? If yes how can I include the wall with its thermal resistance between them. If not, Should I use three separate modules (HT in porous media, solid wall and fluid) for the problem?
What do you suggest? Thank you
Nicolas Huc
November 3, 2016Dear Qasim,
You should keep your existing model with the Conjugate Heat Transfer multiphysics interface and add a Thin Layer feature in the heat transfer model. In the Thin Layer you can specify the thermal resistance. The rest of the model should be kept unchanged.
Oscar Edin
March 6, 2017Hi Nicolas!
I am trying to simulate heat transfer from a helical coil heat exchanger. There are hot water flowing inside the coil and the coil is surrounded by a cylinder where cold water is passed through, causing a cooling effect of the coil. I am using the conjugate heat transfer module for turbulent flow. I’ve set the inlet of the cylinder and the coil with a constant temperature and initial velocity. I have conducted experiments of the same setup and i have noticed that my simulation model is cooled down way faster than for the experiment. For example i have an inlet/outlet temperature of the coil of 30/26 in the experiment, while i get 30/11 in my simulation. Do you have any suggestions whay may cause this and how to fix it?
Nicolas Huc
June 1, 2017Dear Oscar,
I assume that the wall that separates hot and cold water is modeled as a boundary. If it is the case and you believe that the temperature difference between the two sides of the wall is not negligible you can use the Thin Layer feature with Thermally Thick option. This will account for the thermal resistance of the wall for the heat transfer between the hot and cold water. Another suggestion is to use a low-Reynold wall treatment in the flow interface. If it is already the case make sure that the mesh is fine enough (see for example https://www.comsol.com/blogs/which-turbulence-model-should-choose-cfd-application/).
If you would like to discuss further about your model I encourage you to send it to support@comsol.com so that we’ll be able to check it more in details.
With best regards,
Nicolas
Sunku Prasad J
June 29, 2017Dear Nicolas
In case of time dependent conjugate heat transfer model, what is the interface boundary condition between solid and fluid to get the continuous temperature profile?
Nicolas Huc
June 29, 2017Dear Sunku Prasad,
For laminar and low-Reynolds turbulence model, the temperature of the fluid and the solid at the wall corresponds to the same degree of freedom so they are updated simultaneously which makes the temperature profile continuous.
For turbulence model with wall functions the fluid temperature close to the wall is modeled and we use a degree of freedom to compute the fluid temperature close to the wall (but not at the wall). Hence in this case, on boundaries at the interface between a fluid and a solid, the fluid and solid temperatures differ and correspond to different degrees of freedom. The heat transfer between them is determine by the wall function. It is evaluated at every solver iteration so that the temperature at the interface follows the wall function model at every time step.
For more details about COMSOL Multiphysics implementation I recommend reading Heat Transfer and Nonisothermal Flow Interfaces > Theory for the Nonisothermal Flow and Conjugate Heat Transfer Interface chapter in the CFD module Users’ Guide.
With best regards,
Nicolas
Tithi Desai
July 11, 2017I am trying to simulate a thermal sensor, in which I want to add a convection boundary condition on the faces of the sensor, with convection coefficient of 5 W/m^2*K and ambient temperature of 400 deg. C. Would this part of the conjugate heat be useful or is there another way to go about with it ?
Thank you,
Tithi
Nicolas Huc
November 18, 2019 COMSOL EmployeeDear Tithi,
There are indeed different possibilities.
Either you represent only the solid part in the model. And then account for the cooling due to the surroundings fluid using a convective cooling condition on the solid external boundaries.
Or you include the solid and the fluid parts in the model. In this case the solid boundaries become internal boundaries and the convective cooling condition is not used. Instead the flow and temperature profile in the fluid with determine the cooling.
The first approach is less expensive from a computational point of view but it’s accuracy relies on the heat transfer coefficient. If you know the heat transfer coefficient with accuracy then this approach is very efficient.
The second approach is more general. It can give accurate results in configurations where the heat transfer coefficient is not known accurately. Computing accurately the velocity and temperature profile in the flow usually requires significantly more computational resources than the first approach.
I hope it helps,
Best regards,
Nicolas
Basil Srayyih
May 31, 2018Hi Nicolas,
Would you mind if I ask you about the turbulent natural convection inside a cavity filled by a pure fluid (air). Could you help me please how can I write the turbulent dynamic viscosity of the k-e model in the thermal conductivity place of the heat equation by using the user defined?
Thanks and best wishes.
Basil Srayyih.
Nicolas Huc
November 18, 2019 COMSOL EmployeeHi Basil,
If you use the Nonisothermal Flow multiphysics coupling, the effective thermal conductivity accounts for the turbulence through the turbulent thermal conductivity term:
k_turb = C_eff*nu_turb/Pr_turb
(please check the documentation for the notations or for more details about the equations)
In the user interface of the nonisothermal flow coupling you can freely define the turbulent Prandtl number. If you want a different definition for the turbulent thermal conductivity you can directly change the ht.kappaT definition in the Equation View subnode. Then any expression can be used.
Feel free to contact the support if you want to share a model.
Best regards,
Nicolas
Noman Ghulamullah
September 11, 2019Hello , i am working on fuel cells , can i use Conjugate heat module with other modules like tansport of concentrated species , and momentum transport i-e Brinkman equation and navier stokes equation, need some basic example for adding conjugate heat transfer in my model
Nicolas Huc
November 18, 2019 COMSOL EmployeeDear Noman,
I believe everything you need is available. The carbon deposition model (https://www.comsol.com/model/carbon-deposition-in-heterogeneous-catalysis-1968) contains everything you are looking for:
– Heat transfer in free flow and in porous media
– Transport of concentrated species
– Free flow (Navier Stokes)
– Porous media flow (Brinkman)
Best regards,
Nicolas
Malik Awais
November 2, 2019is there any module/solved example available online which solves electronic thermal management of any equipement (https://www.comsol.com/model/forced-convection-cooling-of-an-enclosure-with-fan-and-grille-6222) along with the structural G-loads applied on it under same mesh?? just like any electronic box on an aircraft that is manuvering with 2G or 3G load. It’ll be kind of you if you point me towards the accurate example or set of examples/modules ??
Nicolas Huc
November 6, 2019 COMSOL EmployeeHi Malik,
I suggest to start with this simple tutorial : https://www.comsol.com/model/buoyancy-flow-in-air-53441. It represents natural convection in a box with cold and hot parts. The gravity vector is predefined but you can modify it. Does this corresponds to what you are looking for ?
Best regards,
Nicolas
Ignacio Giménez de Córdoba
May 11, 2020Hi everyone,
I am using a model consisting of a cylinder containing a concentric cylinder of a heating fluid (water that flows at 310 kelvin), a chamber containing a solid (313 kelvin) and the rest of the model is at ambient temperature. I am using the conjugate heat transfer model and the results are not the expected.
– The water flow only heats the entering part, instead of the whole boundaries. When COMSOL plots the temperature, the temperature of the fluid in the upper part just dissapears
– I defined the solid in the chamber as a heating source, but the heat is not transfering to the rest of the model
https://drive.google.com/drive/folders/15sO4Ayr0UB6_RRppwh5clbRIP03bY5ni?usp=sharing
Does anyone know could be wrong here?
Thanks!
Nicolas Huc
May 14, 2020 COMSOL EmployeeDear Ignacio,
I would check that the velocity order of magnitude is correct and check that the nonisothermal flow coupling is active on the fluid domains. If the issue remains, I encourage you to send the model to support@comsol.com to get a detailed feedback.
Ammar Bounemri
July 7, 2020Dear Sir
I use the heat transfer domain in Comsol to achieve results in the field of robotics. For that I would like to know on what is based comsol to work out the analytical equations allowing to have the draw (trace) of the streamlines, in the case of a study of heat transfer from a hot material point to a cold material point. These two points material are assumed to be copper, as example. They are deposited on an environment, also made of copper, of finite dimension. The environment being a form of gaps, that is to say, spaces where there is no material.
I can send you more details on the work I have done so that I can clarify my request for help a little more, if it is necessary.
Nicolas Huc
August 5, 2020 COMSOL EmployeeDear Ammar,
The streamlines plots available in the postprocessing graphs are based on numerical methods. You may notice the Advanced tab in the Streamline plot option where you can control the integration tolerance and the maximum streamline length.
Feel free to reach support@comsol.com and share you model if you have further questions.
Best regards,
Nicolas
Kaleem Iqbal
July 13, 2020Hi, I want to simulate blood flow through stenosis bifurcation arteries with conjugate heat transfer in FSI. Is it possible to do that? If yes, then how to pick BCS.
Nicolas Huc
August 5, 2020Dear Kaleem,
Indeed it is possible to model conjugate heat transfer with FSI. I suggest to check the following tutorial to see how to build the model: https://www.comsol.com/model/bimetallic-strip-in-airflow-74251
Best regards,
Nicolas
Kaleem Iqbal
August 9, 2020Thanks for your suggestion. i go through that tutorial. It is very helpful for dimensional point of view. I got very good results. Is it possible to help me for implementation of dimensionless form of FSI with heat transfer.
Nicolas Huc
August 25, 2020 COMSOL EmployeeHi Kaleem, using the predefined physics for FSI the dependent variables are defined with their units and dimension. However you can control how the solver scales them in the “Dependent Variable” node under the “Solution” node from the solver configurations. The default is “Automatic” and you have other options, in particular Manual that lets you defining the scaling as you wish.
Hannah
August 24, 2020This is a great resource, thank you! I have a question about applying both convective and radiative heat flux to a surface. I currently have a model that uses the thermoelectric effect (heat transfer in solids + electric currents) and I am applying a “general inward heat flux” to the surface through the heat flux boundary condition. I want to vary the amount of convective vs. radiative heat flux that the surface is experiencing. Should conjugate heat transfer be used for this, and/or is there a way to apply known convective and radiative heat fluxes? Thanks!
Nicolas Huc
August 25, 2020 COMSOL EmployeeDear Hannah,
Thanks for your feedback!
Yes, the conjugate heat transfer should be used to define the coupling between heat transfer and the flow, regardless if you want to account for radiation or not. Once the conjugate heat transfer is ready, if you want to account for a radiative heat flux on some surfaces, there are 2 options:
-1- these surfaces are oriented towards the environment, which is at a uniform temperature: in this case you can use the Surface-to-Ambient Radiation boundary condition which is inexpensive from a computational point of view
-2- these surfaces are facing each other or facing objects at different temperatures. In this case you need to compute the view factors between the different parts. This is done using the Surface-to-Surface Radiation physics interface combined with the Heat Transfer with Surface-to-Surface Radiation. This is done for example in the second part of the chip cooling model (https://www.comsol.com/model/electronic-chip-cooling-47721, from page 22 in the pdf – version 5.5).
Hannah
August 25, 2020Thank you! I still have one remaining question though, and one new one:
1. Is there a way to apply a known quantity of convective heat flux? Using the conjugate heat transfer module, I can input the air pressure and velocity to produce a convective heat flux, but would there be a way to either: (a) apply a known amount of convective heat flux, or (b) have the program tell me how much convective heat flux was applied based on those conditions?
2. Can I use surface-to-ambient radiation between my solid domain and my air domain? If so, I know that I can generate radiative heat flux by having them be at different initial temperatures, but is there a way for the program to tell me how much radiative heat flux that resulted in? Since the temperature of the solid surface is changing over time, I can’t just calculate it from the initial temperatures.
Nicolas Huc
September 8, 2020 COMSOL EmployeeDear Hanna,
For the first point, you can check the normal total heat flux and substract the radiative heat flux. Both are predefined variables (ht.ntflux and ht.rflux).
For the second point, I believe ht.rflux is als the quantity you want to check. It is defined on all surfaces where surface-to-surface radiation is active.
With best regards,
Nicolas
Prakash Singh
June 28, 2022I am using laminar flow and heat transfer in the solids and fluids model(conjugate model). I want to simulate a flow between two parallel plates, where the specific heat of plates is temperature-dependent. Also, the heat source I am giving is as follows; heat source=density_solid*Cp_solid(T)*Tad_solid(T)/dt. How can I add this heat source term into the model? How can I determine the temperature distribution in the fluid domain? are heat transfer equations in both domains linked in the conjugate model? Or do I manually have to link both equations?
Nicolas Huc
June 30, 2022 COMSOL EmployeeHi Prakash,
Using the Nonisothermal Flow multiphysics coupling, the heat transfer and the single phase flow physics interfaces are coupled. In particular the temperature field at the fluid/solid interface is handled based on the flow regime and the wall treatment selected in case of turbulent flow. There is no need to do this manually.
Regarding the heat source definition you can either call the functions that define the material properties or directly use the predefined heat transfer variables. In any case the temperature dependency will be accounted for. The operator for the time derivative is “frame”.dt(). See https://doc.comsol.com/6.0/docserver/#!/com.comsol.help.comsol/comsol_ref_definitions.17.028.html for details: “spatial.dt(T) is the time derivative of the field T as seen by an observer that is stationary at fixed coordinates in the spatial frame. Similarly, material.dt(T) is the time derivative experienced by material particles, which are located at fixed coordinates in the material frame”.
An expression like ht.rho*ht.Cp*spatial.dt(T) is supported for the heat source definition.
Don’t hesitate to reach support@comsol.com and share you model if you have further questions.
Best regards,
Nicolas