
As the story goes, Archimedes was struggling with a case of suspected golden crown fraud. While taking a bath, inspiration hit: Submerging an object displaces the same amount of water as the object’s volume, so he could expose any dilutions to the gold. Archimedes was so pleased, he yelled “eureka!” But would anyone have heard the now-famous shout? Using simulation, we can evaluate the acoustics of resonant and reverberant enclosed spaces, like bathrooms, and how they respond to fundamental sources.
Background on Resonances and Reverberant Spaces
When Archimedes shouted “eureka”, a resonance occurred when the wavelength of his voice matched a dimension of the bathroom. When these coincide, the amplitude of the voice becomes very loud. In an enclosed space, there are many resonances, or acoustic room modes, at different corresponding frequencies. Each mode has nodes and antinodes: A node has zero acoustic pressure, while an antinode is located where the pressure is at maximum.

Illustration of Archimedes’ “eureka” moment in the bath, where he is said to have coined the term. Image by John Leech and in the public domain, via Wikimedia Commons.
Resonances are often associated with large responses. However, if a monopole lies on a node, no noise will be generated; monopoles are most efficient when they lie on an antinode. Conversely, a dipole will produce no sound if it is positioned on an antinode, but it will produce a strong response if it is located at a node. You can find the modes of your own bathroom by performing an oral frequency sweep (also known as singing in the shower) while listening for unexpected increases in loudness at certain pitches.
Reverberant spaces have many reflections of acoustic waves that are not absorbed efficiently at boundaries. Reverberations are similar to echoes; they differ because echoes are discretely distinguishable from other finite echoes. Reverberation has a large impact on the clarity of speech in a space: A shorter reverberation time gives crisper, clearer, and cleaner acoustics than acoustically muddy spaces, such as cathedrals. You can experiment with reverberant spaces by clapping your hands and counting how long you can hear the noise decay.
Predicting Resonances with COMSOL Multiphysics®
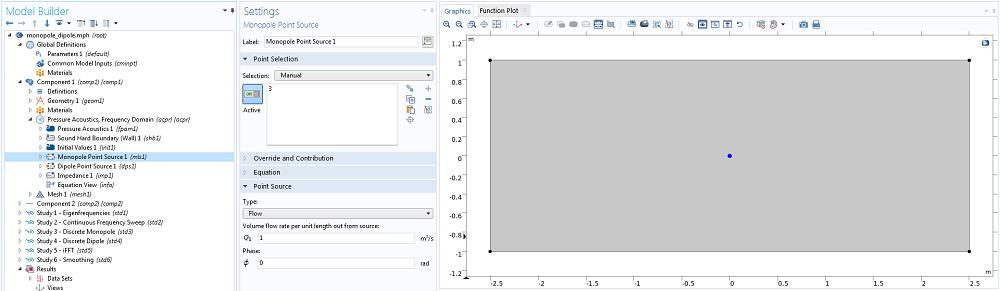
The first step in investigating the acoustics of enclosed spaces is to draw the geometry of the bathroom. Here, the bathroom is aggressively defeatured to a 2-by-5 m rectangle with a point in the center. Initially, we find the first few mode shapes and frequencies. Once these are established, a monopole and dipole are placed on a node and antinode to investigate the responses.
Eigenfrequency Predictions
The Pressure Acoustic, Frequency Domain interface is applied to the rectangle, and the frequency domain form of the equations implements the stationary Helmholtz representation. The boundary conditions on the rectangle are unchanged from the default, acoustically rigid boundaries; therefore, the model is lossless. The geometry and interface are shown below.
The canonical representation of the bathroom geometry, showing the location of the monopole and dipole.
The first study solves for the eigenfrequencies of the domain, and these eigenfrequencies correspond to the acoustic modes of the rectangle. Note that when solving for eigenfrequencies, any source that has been applied to the model will be ignored; i.e., it is the roots of the homogeneous form of the equation that are sought. The modes of the space are determined by the length and boundary conditions of the domain. Analytic solutions can be derived to confirm the numerical approximations for this canonical problem.
The figure below visualizes the first two mode shapes of the enclosed space. They show that a node and an antinode lie on the x = 0 line for the first and second modes, respectively. For this geometry, the two mode frequencies are 34 Hz and 68 Hz. The actual frequencies are unimportant, so they will not be referred to by value in this post.
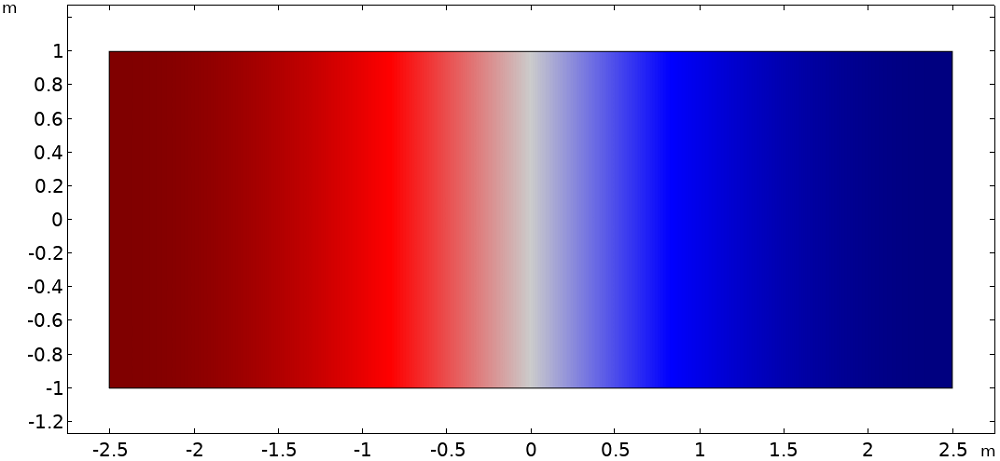
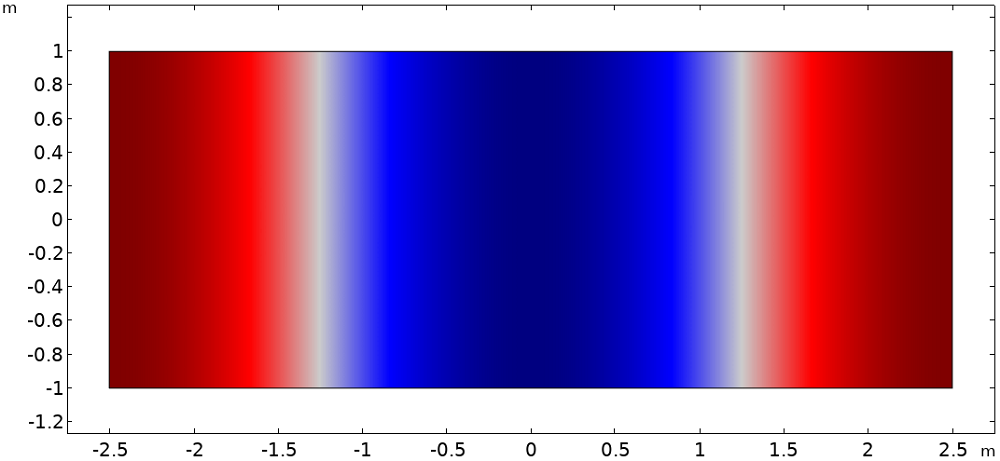
Normalized pressure of the first two modes of the enclosed space. We have zero pressure on a node (left, midway) and maximum pressure on an antinode (right, midway).
Fundamental Sources in Enclosed Spaces
With the mode shapes and associated frequencies established, the next step is to add the monopole and dipole to the point at the center of the geometry. The dipole is aligned in the x direction. In two frequency domain study steps, the monopole and the dipole are excited over an appropriate frequency range. The results are normalized in postprocessing so that both sources have unit amplitude.
To evaluate the effect of the enclosed space on the fundamental source, the sound pressure level (SPL) is averaged. To implement this, the Average component coupling is applied to the domain. This coupling calculates the spatial arithmetic average of a variable.
The average SPLs in the enclosed space due to the different fundamental sources are displayed below. The plot shows that each source has an enormous increase in the average SPL (more than 80 dB) at one of the two modes. It demonstrates that the monopole has little effect at the first mode, but there is a very large response when it lies on an antinode. The response is vice versa for the dipole. For simple models, this result can be confirmed by analytic predictions.
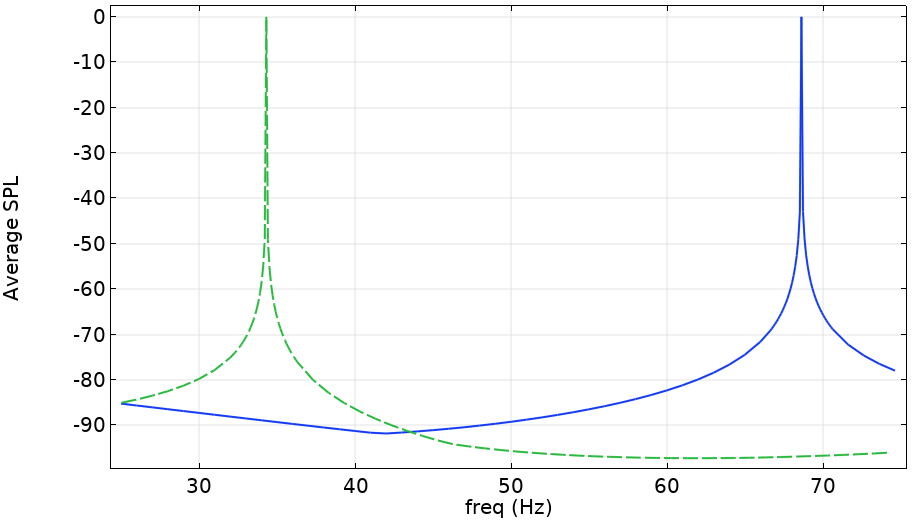
The average SPL for two fundamental sources. The blue line is a monopole and the green dashed line is the dipole loading. Both sources lie in the middle of the enclosed space.
Alternatively, the sources can be loaded at the exact value of the eigenfrequencies. This can be done by changing the form of the equation from Study controlled to Frequency domain under the Settings panel for the interface. The applied frequency can then be prescribed using withsol('sol1',real(freq),setind(lambda,N)). This means: use from (withsol) Solution 1 ('sol1') and set the frequency (real(freq)) to be the eigenvalue (lambda) from indices ( N is equal to one and two). The offset of 1e-3 Hz is required because the model is lossless and is mathematically poorly defined at resonance, and consequently, a solution is not returned.
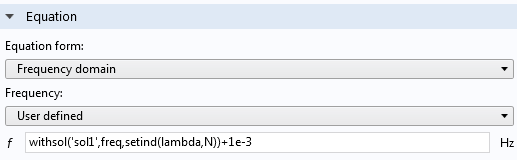
The required edit to load the model at a precise eigenfrequency found in COMSOL Multiphysics.
When this method is implemented, the average SPL in both fundamental source cases is approximately 87 dB lower for one mode compared to the other.
Thoughts on Predicting the Resonance of an Enclosed Space
The significance of our resonance investigations can be concluded to: If Archimedes and his bath were infinitesimal, located on a node, and had monopole noise directivity characteristics, few would have heard Archimedes’ insights when he shouted “eureka.”
Modeling Reverberations in Enclosed Spaces
The reverberation of an enclosed space can be quantified by simulating a transient fundamental source and measuring the SPL over time. The monopole can be approximated by a spherical array of speakers. A common metric used by architectural acousticians is to measure the T60 value of a room — the amount of time it takes for the sound field to decay by 60 dB.
Ray theory can be used to predict the impulse response of an enclosed space; however, this approximation is only valid in the high-frequency limit. This approximation is not valid for acoustically small and enclosed spaces, such as Archimedes’ bathroom. Luckily, the finite element method (FEM) can be used to calculate the low-frequency response, and this low-frequency response can then be passed into an inverse fast Fourier transform (iFFT) routine to generate a low-frequency impulse response due to a fundamental or distributed source.
Low-Frequency Response to a Monopole
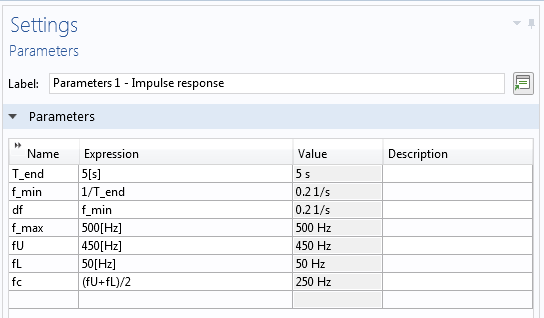
When obtaining impulse predictions, the parameters shown in the left screenshot below are used to speed up the modeling process.
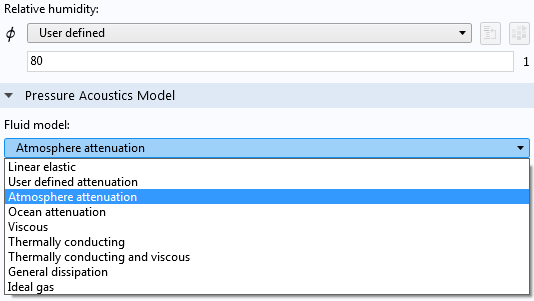
Parameters (left) and the attenuation model (right) used in the reverberant model.
The Fluid model is changed from the default Linear elastic (which contains no losses) to Atmospheric attenuation. This model of attenuation is based on a semiempirical model. The relative humidity is set to 80, a high value due to the warm bath. Also, the boundaries are changed to be slightly lossy impedance boundaries.
The dipole is disabled, and the monopole is loaded at the frequencies given from the parameters. The study is performed in two steps, with the second taking the frequency response results of Study 1 and performing an iFFT on the windowed results. The animation below shows the total instantaneous pressure due to the monopole oscillating at the centerband frequency of 250 Hz. At this frequency, it is clear that the wavelength is not in the high-frequency limit for a geometry of this length.
Instantaneous pressure at 250 Hz due to the monopole source at the center of the domain.
Impulse Response Predictions
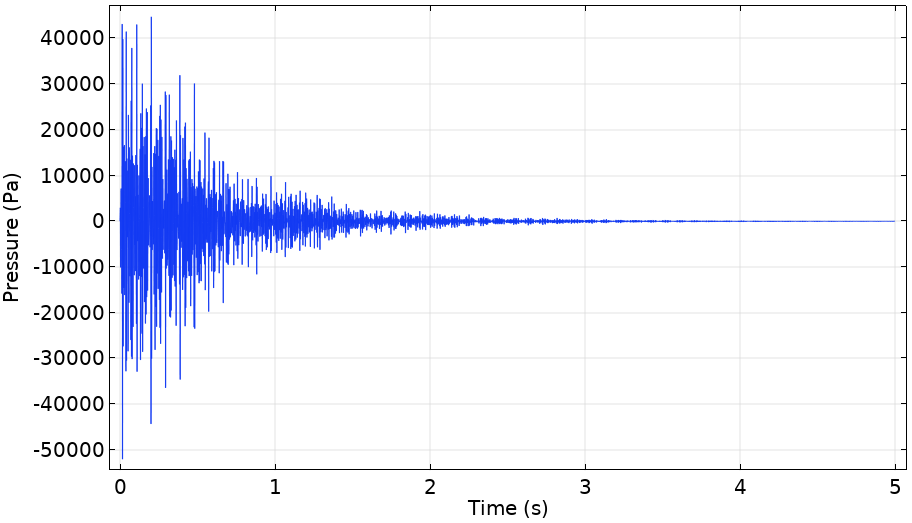
The left image below shows the instantaneous pressure generated by the iFFT. As is expected, the logarithm of the raw data is noisy, so a Gaussian average is implemented to smooth the signal, shown on the right. The convolution integral of the built-in Gaussian pulse function and the iFFT data are implemented by laying the pulse and the iFFT data along a 1D component and integrating (the appropriate integrand) over the line using a line integral component coupling.
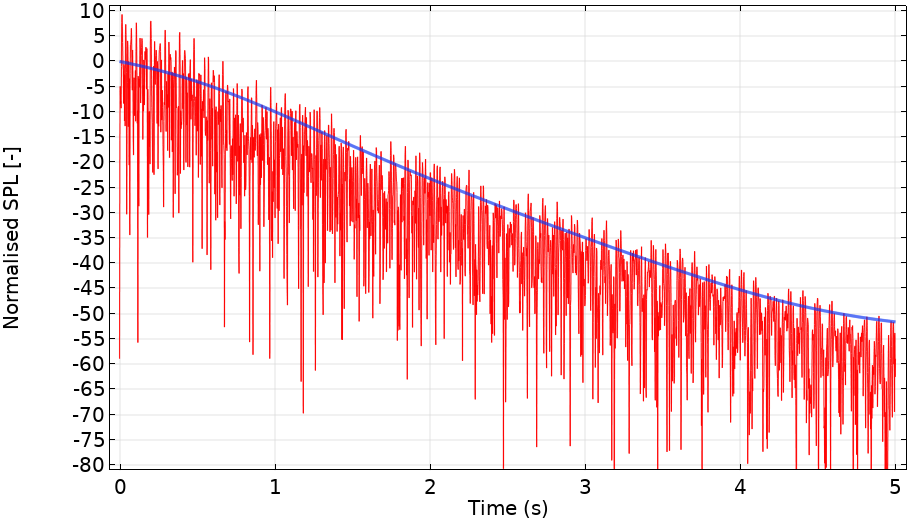
On the left is the instantaneous pressure from the iFFT of the FEM predictions at low frequencies. On the right, the red line is the logarithm of the instantaneous pressure, while the blue line is the smoothed version of the red line.
The smoothed logarithm of the pressure is roughly linear in the middle of the time period. By extrapolating this regime, the figure demonstrates that the bathroom has a T60 value of approximately 6 s. This would suggest that conversation would be difficult in Archimedes’ bathroom but, had they been invented, Gregorian chants would sound splendid.
To confirm our result, we can compare it to a simple method of predicting T60 methods valid for modes. We can estimate the T60 value of a mode by multiplying the imaginary component of the eigenfrequency by 0.9. In this case, the centerband frequency of the iFFT study is 250 Hz and the nearest mode is 255 Hz. This mode will dominate the response and has an associated T60 value of 5.9 seconds.
The method presented here is valid for low frequencies; however, if the applied frequencies are in the high-frequency limit, then the Ray Tracing interface could be used. In addition, if the sound field was disperse and three dimensional, we could use the Acoustic Diffusion Equation interface to obtain the T60 values of the various analytic models or calculate it directly.
Concluding Thoughts
In this blog post, we have used COMSOL Multiphysics and add-on Acoustics Module to model monopoles and dipoles in a very simple enclosed space. We have demonstrated an interesting phenomenon where fundamental sources produce essentially no sound when placed at certain locations and frequencies in an enclosed domain. In addition, we have used FEM to predict the low-frequency T60 value without resorting to the often specious ray approximation.
Next Steps
Learn about the specialized features for acoustics modeling available in the Acoustics Module by clicking the button below.
Related Resources
- Try modeling the acoustics of enclosed spaces with these examples:
- Read how engineers created a simulation test bench for decay times in room acoustics in a paper presented at the COMSOL Conference 2018





Comments (0)