
Behind the wheel of a car is not the ideal place to discover that the steering wheel is defective. That’s why special precautions are taken during the manufacturing process. The carefully controlled cooling of an injection mold ensures that whatever the product may be, its standards are up to par. Here, we use the Non-Isothermal Pipe Flow interface with the Heat Transfer in Solids interface to study the cooling path of an injection mold for a polyurethane car steering wheel.
Introduction to Injection Mold Manufacturing
Injection molding is the most common form of polymer manufacturing because of the speed and ease of producing large amounts of product. The process was first patented by brothers John Wesley and Isaiah Hyatt in 1872. During World War II, injection molding rapidly expanded due to the need for mass produced goods made quickly. Injection mold manufacturing has steadily grown over time with the constant development of new manufacturing materials.
Cooling takes up over 50% of the time in an injection mold cycle, and it is an important step in the manufacturing process. Improper cooling can lead to blistering (raised regions on the surface of the product), sink marks or “sinks” (depressions in a region of the product), and even warping or twisting in the product. Without proper cooling, the resulting deformed or defective products waste time, money, and materials. And assuming that a number of products made by injection molding are used for important functions, such as car steering wheels, producing defective products can be dangerous.

A polyurethane steering wheel.
Modeling the Cooling of an Injection Mold
What we are modeling here is the top half of the wheel grip on a steering wheel, which is made from polyurethane. The mold for the product is a 50-by-50-by-15 centimeter steel block with two cooling channels that are each one centimeter in diameter. Keep in mind that the properties and positioning of the cooling channels are important aspects in the results. For our simulation, the average temperature of the mold after injection is 473 K. Water at room temperature is used as cooling fluid and flows at a rate of ten liters per minute. The simulation takes ten minutes to set up and run.
For the Non-Isothermal Pipe Flow interface, momentum and mass equations describe the flow in the cooling channels. The Churchill Friction model calculates pressure drop due to viscous shear. This calculation can be used for both laminar and turbulent flow and it is predefined in the interface.
The temperature distribution and heat transfer of the cooling water in the pipe are calculated in the Non-Isothermal Pipe Flow interface. The heat transfer and temperature distribution in the steel block and polyurethane product are calculated with the Heat Transfer in Solids interface, which seamlessly couples to the pipe calculations. Additionally, COMSOL Multiphysics 5.0 can automatically determine if the pipe flow is laminar or turbulent and automatically adjust pressure drop and heat transfer properties accordingly.
The Results
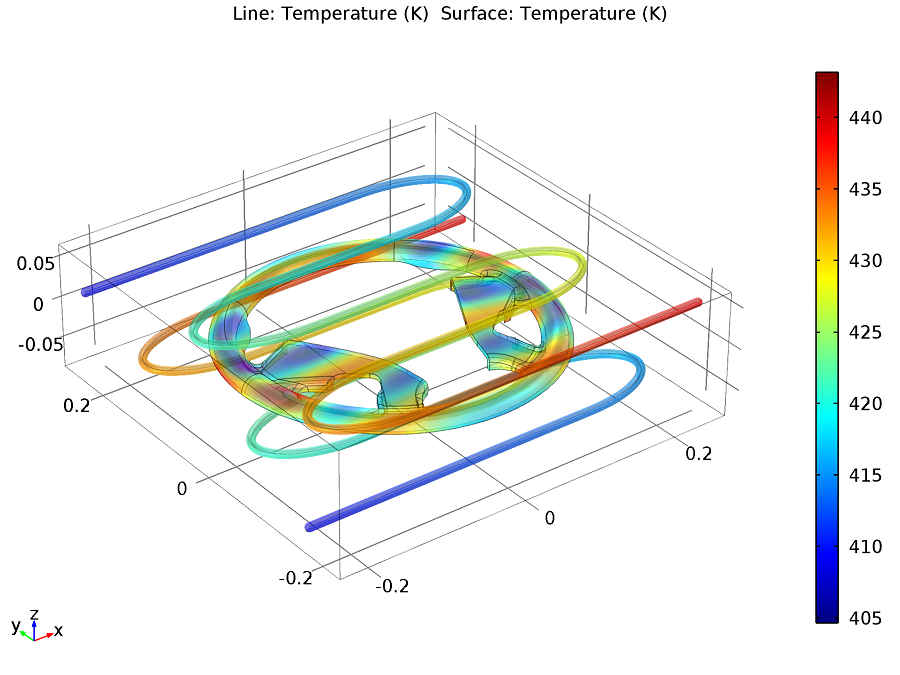
After two minutes of water flow through the channels, there is still a fair amount of cooling needed. The hottest and coolest regions of the mold differ by about 40 K.
The temperature distribution in the polyurethane steering wheel (left) and the entire steel mold (right) after 2 minutes of cooling.
After 10 minutes, the steel mold has a more uniform temperature, but there is still a 20 K difference in temperature at the inlets and outlets of the cooling channels.
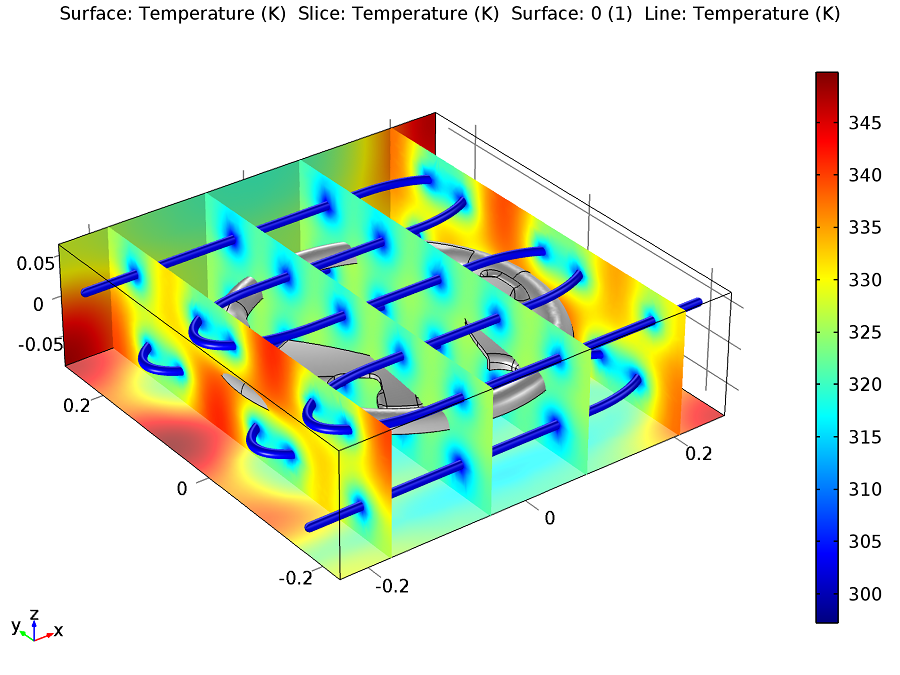
The injection mold after 10 minutes of cooling.
With simulation software, we can easily change different factors to provide additional information. After the initial simulation, we can vary the flow rate of the water, surface roughness of the cooling channels, and the material of the mold to investigate different cooling paths of the mold.
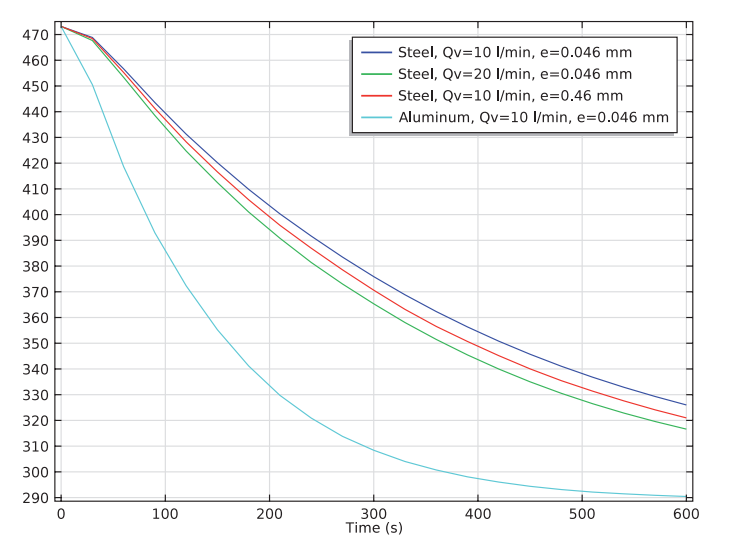
The temperature of the polyurethane steering wheel varies as different factors change.
Results indicate that the thermal conductivity of the mold material is the most important factor for fast cooling in injection molding, where changing the mold material from steel to aluminum reduces the cooling time significantly. On the other hand, increasing the flow rate from 10 l/min to 20 l/min reduces the cooling time a bit, whereas the increase in cooling efficiency from increasing the surface roughness of the cooling channels by a factor of 10 was marginal and may not warrant the pressure drop this results in.
Further Reading
- Try it yourself: Download the Cooling of an Injection Mold model
- Blog post: How to Easily Connect 1D Pipes to 3D Flow Domains







Comments (3)
Francisco Moraga
March 23, 2021Brianne,
I tried this model for a problem which also has embedded pipes in metal that heats up the flow in the pipe. The model runs in minutes instead of the hours needed if the pipe flow is computed with a 3D RaNS model and it is much more robust. However even at large inlet Reynolds numbers, like 40,000 the two models give considerably different results. It very well may be because of coarse grids. But before going into grid convergence studies I would like to understand better how the solid and pipe flow interact and the grid requirements for the metal in the region of interaction. How the temperature of the metal used to compute heat transfer to the flow is computed? Is the pipe diameter used to decide what cells in the metal provide the temperature? if so, is there a grid topology around the pipe that it is more convenient?
Brianne Christopher
March 26, 2021Hi Francisco,
For the 3D simulation, the heat exchange between the pipe and the metal depends on the turbulence model and wall boundary conditions used in the simulation. If the turbulence model uses wall functions or automatic wall treatment, thermal wall functions will be used inside the pipe. In practice, this means that a heat flux (based on the difference between the temperatures of the physical wall and the outer boundary of the flow domain, which are different, since the latter is displaced by an applied offset) is applied to the fluid in the pipe, and the temperatures on the fluid and solid at the physical wall are constrained to be equal. If a low-Reynolds-number wall treatment is used, the temperature and the heat flux automatically become continuous, since they share the degrees of freedom on the boundary.
For pipe flow simulations, a heat flux based on the difference in temperature between the pipe and the solid is applied on both sides. An operator, applying an average over a disk of the same cross section as the pipe, is used when applying the heat flux on the solid domain.
Regarding mesh resolution: In 3D models, the wall distance (or distance to the first cell center) is usually supplied as a postprocessing variable in the fluid flow interface. This value should be around 1 for low-Reynolds-number wall treatment and can be up to 50 for automatic wall treatment and wall functions. For pipe flow simulations, the mesh resolution in the solid should be of the same size as the physical pipe radius in the vicinity of the pipe. In both cases, depending on inlet and outlet boundary conditions, there may also be sharp gradients along the pipe that need be resolved.
The accuracy of the heat exchange between the pipe and the solid also depends on the wall treatment and the mesh resolution. In general, a properly resolved model with a low-Reynolds-number treatment will give the most accurate results. This, however, becomes prohibitively expensive when the Reynolds number is large, and a wall functions approach can give sufficient accuracy.
If you need further assistance, please send your model to support@comsol.com.
Best regards,
Brianne
Francisco Moraga
March 23, 2021Another relevant question is how the accuracy of the temperatures in the mold depends on the ratio of the pipe diameter and a characteristic dimension of the mold. does the accuracy increases as the ratio diminishes?